11724. Infected tree
You are given a binary tree, which is an
acyclic connected undirected graph containing n vertices and n
– 1 edges. Each vertex has a degree of no more than 3. The root is the
vertex number 1, with its degree not exceeding 2.
Unfortunately, the root of the tree is
infected. The following process is repeated n times:
·
Huseyn
either selects a vertex that is not yet infected (and not yet removed) and
removes it along with all its incident edges, or he takes no action.
·
After
that, the infection spreads to every vertex connected by an edge to an already
infected vertex (all previously infected vertices remain infected).
Help Huseyn determine the maximum number of
vertices he can save from infection (note that removed vertices are not
considered saved).
Input. The first line contains the number of vertices in the tree n (2 ≤
n ≤ 3 * 105).
Each of the following n – 1 lines
contains two integers ui and vi (1 ≤ ui,
vi ≤ n), representing an edge of the tree.
It is guaranteed that the graph is a binary
tree with the root at vertex 1.
Output. Print a single integer – the number of saved vertices.
|
Sample input 1 |
Sample output
1 |
|
4 1 2 2 3 2 4 |
2 |
|
|
|
|
Sample input 2 |
Sample output
2 |
|
7 1 2 1 5 2 3 2 4 5 6 5 7 |
2 |
SOLUTION
tree – dynamic
programming
Algorithm analysis
For each vertex v, compute the number of
vertices sum[v] in the subtree where it is the root. If to1, to2,
…, tok are the
children of vertex v, then
sum[v] = 1 + sum[to1]
+ sum[to2] + … + sum[tok]
If vertex v is a leaf of the tree, then sum[v] = 1.
Let dp[v]
be the number of saved vertices in the subtree with root v, assuming that currently vertex v (and only it in the subtree) is infected.
If vertex v has only one child to,
then dp[v] = sum[to] – 1 (the removed vertex to is not considered saved).
Let vertex v have two children to1 and to2 (each vertex has a degree of at most
3). Then we have two options:
·
Remove
to1 and recursively save the vertices in the subtree with
root to2. The number of saved vertices will be sum[to1] – 1 + dp[to2].
·
Remove
to2 and recursively save the vertices in the subtree with
root to1. The
number of saved vertices will be sum[to2] – 1 + dp[to1].
Among the two options,
choose the one that maximizes the number of saved vertices.
Consider the depth-first
search process when examining the edge (v, to).
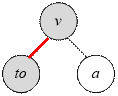
Let a be the second
child of vertex v. We need to compute the value dp[to] + sum[a] – 1. Let’s try to find it using only the vertices v and to.
We know that:
sum[v] = 1 + sum[to] + sum[a]
From which it follows that:
sum[a] = sum[v] – sum[to] – 1
Thus,
dp[to] + sum[a] – 1 = dp[to] + sum[v] – sum[to] – 2
Iterate over the children to of the vertex v and compute:
dp[v] = max(dp[to] + sum[v] – sum[to] – 2)
Example
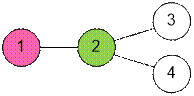
In the first example, Huseyn is able to
save two vertices, 3 and 4, by choosing vertex number 2 as his first move.
Consider the second example. Next to each
vertex v, place the labels sum[v] / dp[v]. The vertices chosen by Huseyn are displayed
in green.
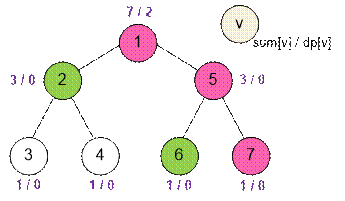
For example,
dp[1] = max(sum[2] – 1 + dp[5], sum[5] – 1 + dp[2]) =
max(2, 2) = 2,
sum[1] = 1 + sum[2] + sum[5] = 1 + 3 + 3 =
7
Algorithm implementation
Declare
the arrays.
#define MAX 300005
int sum[MAX], dp[MAX];
vector<vector<int>> g;
The
function dfs performs a depth-first search starting from vertex v.
The parent of vertex v is p.
void dfs(int v, int p = -1)
{
Initialize
the variables sum[v] and dp[v].
sum[v] = 1;
dp[v] = 0;
Perform
a depth-first search starting from the children of
vertex v.
for (int to : g[v])
if (to != p)
{
dfs(to, v);
sum[v] += sum[to];
}
Compute
the value of dp[v].
for (int to : g[v])
if (to != p)
{
dp[v] = max(dp[v], sum[to] - 1); // if 1 son
dp[v] = max(dp[v], dp[to] + sum[v] - sum[to] - 2);
}
}
The
main part of the program. Read the input data.
scanf("%d", &n);
g.clear();
g.resize(n + 1);
memset(dp,
0, sizeof(dp));
memset(sum,
0, sizeof(sum));
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
Perform
a depth-first search starting from vertex 1.
dfs(1);
Print
the answer.
printf("%d\n", dp[1]);